St. Petersburg, Russian Federation
Russian Federation
Moscow, Russian Federation
St. Petersburg, Russian Federation
UDC 699.852.7
CSCSTI 67.01
Objective of the article is to determine the dependence of stresses on the surface of the coating plate of a special structure under the influence of an explosion, the parameters of the protective structure modified with a cement-sand matrix. Important aspects of this work are the geometric characteristics of the auxetic structure, as well as the strength properties of the concrete composite, which is represented by strength classes B30, B45 and B60. The study used the following methods: numerical modeling, statistical analysis and experimental planning in the ANSYS Explicit Dynamics software package, where the cement-sand matrix was described by the Drucker-Prager strength criterion. The study found that protective structures with round and square voids are not able to protect the coating plate of a special structure when exposed to an explosion. On the contrary, plates with auxetic construction have demonstrated their effectiveness, significantly absorbing energy during explosive impacts. When calculating for 27 different combinations of factors, ANSYS Explicit Dynamics obtained stresses in the coating plate ranging from 22 to 81 MPa. Based on these data, regression analysis was performed, which made it possible to construct a mathematical model in the form of a polynomial equation of the second degree. This model combines the stress level (Y) with three key factors: the ratio of the cell area to the system (x₁), the ratio of the void area to the material (x₂) and the strength of the concrete (x₃). The adequacy of the obtained model was confirmed by the Fisher criterion, where the calculated value of F $$(F_c = 19.0811)$$ is higher than the tabular value $$(F_t = 1.9881)$$. This indicates the ability of the model to adequately describe the process under study. The created regression model makes it possible to more accurately select the parameters of energy-absorbing structures at the design stage. The establishment of optimal geometric parameters of an auxetic structure provides an opportunity to develop protective structures that significantly increase the resistance of a special structure to explosive impacts, which helps to increase the survivability of significant objects and reduce damage from dynamic loads.
stresses, coating plate of a special structure, protective structure, cement-sand matrix, auxetic structure, mathematical modeling, regression analysis, regression equation, Fisher criterion, dynamic impact, optimization of parameters
Введение
Данное научное исследование представляет собой сравнительный анализ эффективности различных типов защитных конструкций (ЗК) для специальных сооружений (СС) от взрыва. В рамках работы были смоделированы ЗК, основанные на цементно-песчаной матрице (ЦПМ) c классами прочности В30, В45, В60, где ЦПМ описывалась критерием прочности Друкера-Прагера [1], ауксетическая структура [2-9], а также структуры с квадратными и круглыми пустотами, что иллюстрируется на Рис 1.
Основной целью анализа стала оценка способности ЗК к энергопоглощению [4,9], что является важным для обеспечения безопасности СС в условиях действия взрывов. В ходе проведенного анализа выяснилось, что, несмотря на то, что геометрические параметры ауксетических пустот [3] имеют относительно низкие показатели прочности по сравнению с пустотами круглой и квадратной формы, их деформативность оказывается ключевым фактором, способствующим повышению значения энергопоглощения.
Это открытие позволило с высокой степенью уверенности проводить математическое моделирование и анализ функциональных характеристик ЗК, выполненных из композитных материалов на основе измененной ЦПМ.

Рис. 1. Модифицированная ЦПМ: а) с квадратными пустотами,
б) с круглыми пустотами, в) с ауксетической возвратно-вогнутой структурой
На данном этапе было установлено, что традиционные решения плит с круглыми (Рис. 2, г) и квадратными пустотами (Рис. 2, в), а также с воздушной прослойкой (Рис. 2, б), не гарантируют требуемого уровня защиты, приводя к полному пробитию плиты покрытия и уничтожению несущих конструкций.
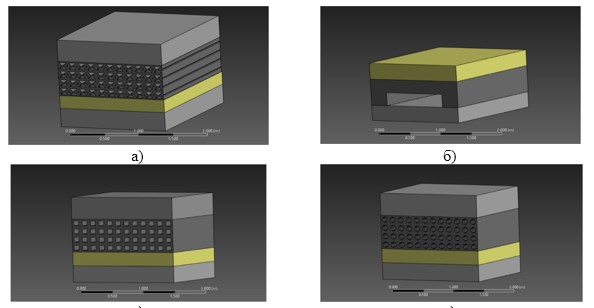
Рис. 2. Вид защитной конструкции: а) с ауксетической структурой,
б) с невесомой прослойкой, в) с квадратными пустотами, г) с круглыми пустотами
В то же время была испытательно подтверждена высокая эффективность защитных плит с ауксетической конструкцией (Рис. 2, а), которые за счет уникальной геометрии ячеек демонстрируют способность эффективно поглощать энергию взрыва, сохраняя целостность основной системы [9]. Преимущество ауксетических структур [3] определило необходимость более основательного изучения влияния их геометрических и физико-механических параметров на напряженно-деформированное состояние ЗК (Рис. 3).

Рис. 3. Результат воздействия взрыва на плиту СС:
а) при ЗК с ауксетической структурой, б) при ЗК с воздушной прослойкой,
в) при ЗК с квадратными пустотами, г) при ЗК с круглыми пустотами
С использованием численного моделирования в программном комплексе ANSYS Explicit Dynamics была совершена оценка напряженно-деформированного состояния защитной плиты и плиты покрытия. Это позволило получить результаты, которые показывают, что существующие ЗК не обеспечивают необходимую защиту. В частности, плита покрытия СС оказывается полностью пробитой ударной волной, образующейся в результате взрыва.
Для достижения цели исследования был применен методы математического моделирования, включающий экспериментальное планирование. Это позволяет оценить влияние различных факторов на эффективность ЗК. Были изучены такие параметры, как отношение площади ячеек к конструкции (обозначаемое как X1 = Sя/Sк), отношение площади пустот к площади материала (X2 = Sп/Sм) и прочность бетона (X3). На основе данных, полученных в ходе моделирования в ANSYS Explicit Dynamics, был проведен регрессионный анализ с целью создания математической модели. Значимость результатов была установлена с применением критерия Фишера. Это позволяет уверенно говорить о достоверности полученных значений. В результате анализа удалось не только установить аналитическую связь, но и определить оптимальные геометрические параметры ауксетической структуры, которые минимизируют нагрузку. Это доказывает целесообразность использования таких систем для повышения защитных свойств СС, предназначенных для защиты от техногенных нагрузок.
Математическое описание зависимости напряжений, образующихся на поверхности плиты покрытия СС
В процессе математического прогнозирования с использованием ANSYS Explicit Dynamics была изучена зависимость напряжений в ауксетически модифицированной плите от влияния взрыва на геометрические параметры возвратно-вогнутой ауксетической текстуры [3] и прочностные свойства используемых конструкционных материалов. В результате были определены значения напряжений на поверхности плиты с покрытием для разных конфигураций защитной конструкции, как показано в Таблице 1.
Таблица 1
Данные математического прогнозирования динамического воздействия
|
№ испытания |
Х1 |
Х2 |
Х3 |
Y |
|---|---|---|---|---|
|
1 |
0,005 |
0,5 |
30 |
6,2 |
|
2 |
0,01 |
0,5 |
30 |
7,9 |
|
3 |
0,015 |
0,5 |
30 |
7,6 |
|
4 |
0,005 |
0,79 |
30 |
5,2 |
|
5 |
0,01 |
0,79 |
30 |
6,0 |
|
6 |
0,015 |
0,79 |
30 |
4,9 |
|
7 |
0,005 |
1,5 |
30 |
4,2 |
|
8 |
0,01 |
1,5 |
30 |
3,2 |
|
9 |
0,015 |
1,5 |
30 |
2,9 |
|
10 |
0,005 |
0,5 |
45 |
6,4 |
|
11 |
0,01 |
0,5 |
45 |
8,0 |
|
12 |
0,015 |
0,5 |
45 |
7,7 |
|
13 |
0,005 |
0,79 |
45 |
5,0 |
|
14 |
0,01 |
0,79 |
45 |
6,1 |
|
15 |
0,015 |
0,79 |
45 |
3,9 |
|
16 |
0,005 |
1,5 |
45 |
4,0 |
|
17 |
0,01 |
1,5 |
45 |
3,0 |
|
18 |
0,015 |
1,5 |
45 |
2,5 |
|
19 |
0,005 |
0,5 |
60 |
6,6 |
|
20 |
0,01 |
0,5 |
60 |
8,1 |
|
21 |
0,015 |
0,5 |
60 |
7,8 |
|
22 |
0,005 |
0,79 |
60 |
5,0 |
|
23 |
0,01 |
0,79 |
60 |
6,1 |
|
24 |
0,015 |
0,79 |
60 |
3,8 |
|
25 |
0,005 |
1,5 |
60 |
3,7 |
|
26 |
0,01 |
1,5 |
60 |
2,7 |
|
27 |
0,015 |
1,5 |
60 |
2,2 |
Произведена математическая обработка результатов (Рис. 4).
|
$$\sigma x_i=2\cdot\frac{x_i-\frac{x_{imax}+x_{imin}}{2}}{x_{imax}-x_{imin}} ,$$ |
(1) |
где δXi — нормированное значение i-го фактора;
Xi — значительность i-го фактора, в натуральных единицах;
Xi max и Xi min — максимальное и минимальное значения i-го фактора в соответствии с этим, в натуральных единицах.
Добавив стандартизованные коэффициенты в уравнение регрессии, оно будет иметь вид:
|
|
(2) |
где δYj выч — нормированное значение j-го свойства ЦПМ;
a0, a1 — стандартизованные коэффициенты регрессии …, an.
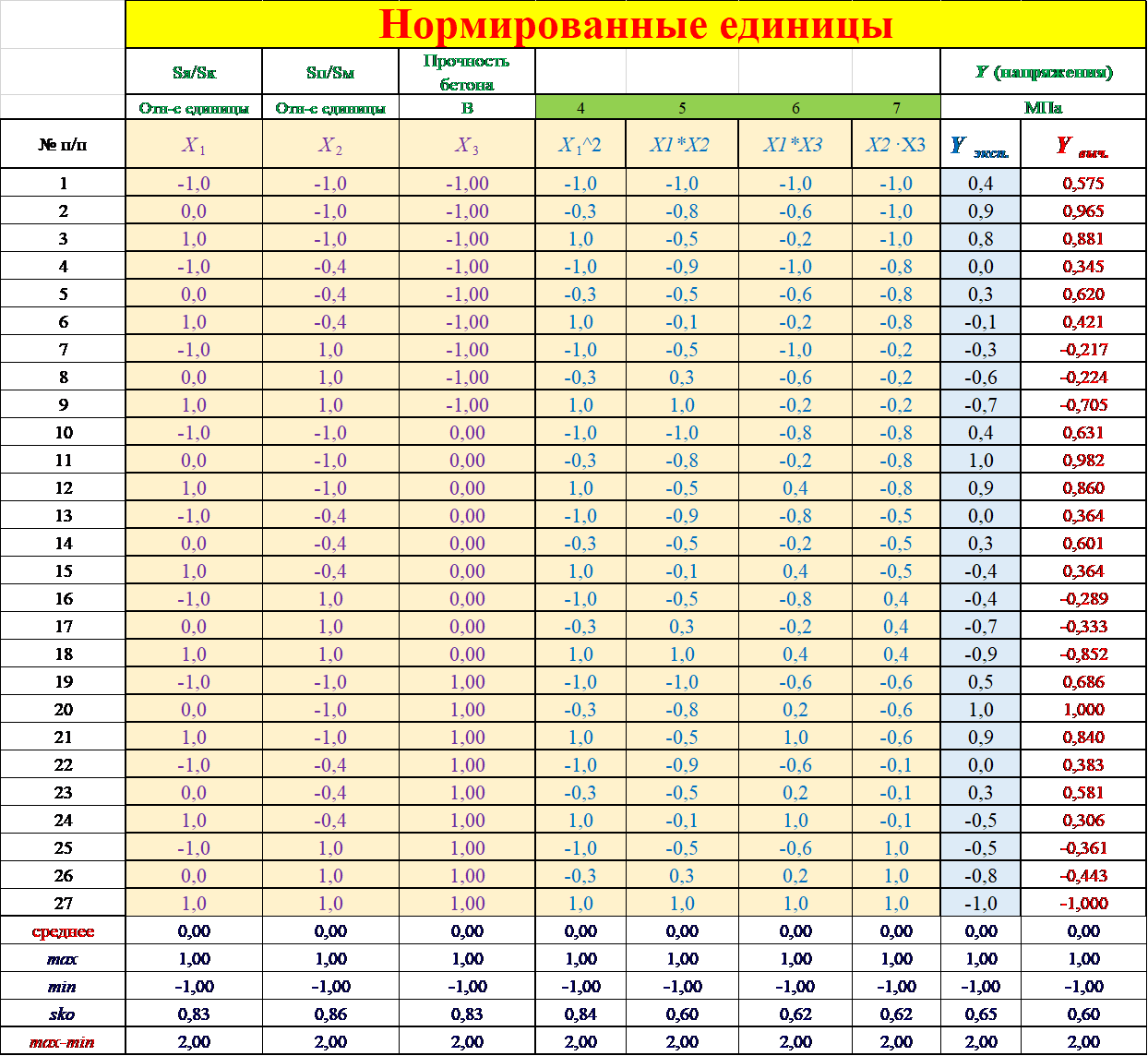
Рис. 4. Массив данных в нормированном виде
Применив критерий Фишера прошло проверку значимости и показало доверительную вероятность α = 0,95.
В процессе обработки экспериментальных данных, было составлено уравнение регрессии (математическая модель), которое адекватно описывает зависимости напряжений, на поверхности плиты покрытия СС, от множества факторов. Такие, как Х₁, Х₂ и Х₃, и визуализация этой зависимости была представлена на Рис. 5.
Y= -0,448 + 1,396·X1 – 0,071·X2 + 0,16·X3-0,962 X12 –
– 0,805 X1·X2 – 0,192 X1·X3 – 0,323 X2·X3
Fрасч = 19,0811, Fтабл = F (26, 23) = 1,9881
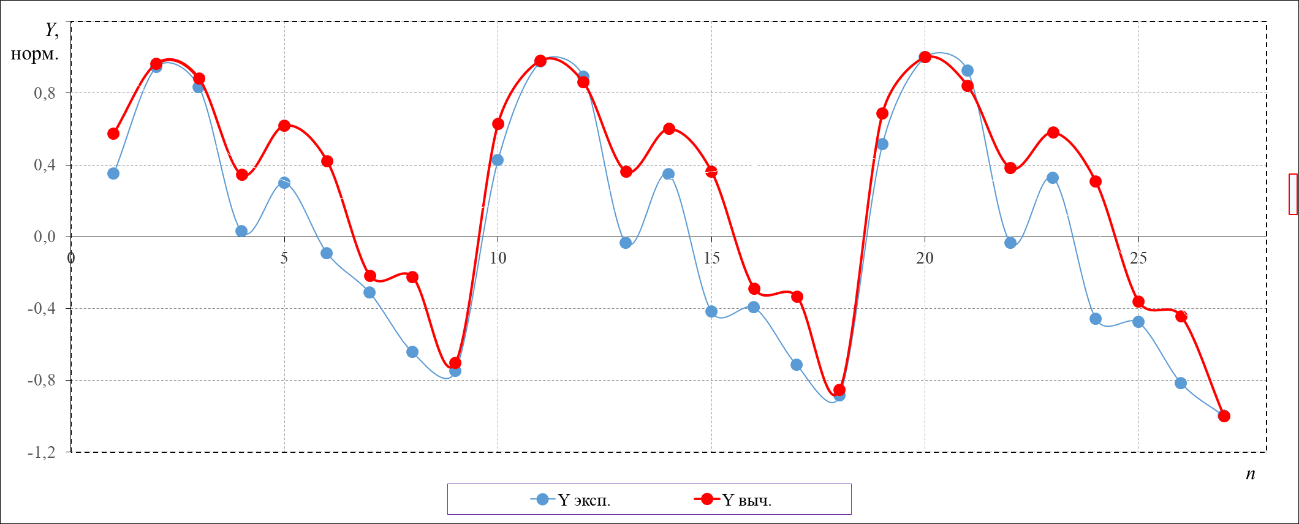
Рис. 5. Диаграмма экспериментальных и расчетных значений
В ходе работы было установлено, что расчетное значения (Fрасч) превышает табличное (Fтабл), что указывает на статистическую точность уравнения регрессии. Из этого следует, что разработанная математическая модель показывает влияние факторов Х1, Х2 и Х3 на способность модифицированной ЦПМ выполнять свою защитную функцию. Анализ показал, что при максимальном увеличении толщины стенки до 8,6 мм и шестикратном повышении ячейки покрытие СС испытывает минимальные динамические нагрузки. Оптимальный показатель, зафиксированный в ходе эксперимента, составил 2,25 МПа, что соответствует напряжениям в покрытии плиты СС, вызванных взрывом. Это значение является важным признаком, поскольку показывает, насколько эффективно покрытие выдерживает динамические действия и подтверждает правильность выбранных параметров для увеличения защиты СС. Из проведенных исследований можно сделать вывод, что ЗК СС ауксетического типа (ВВС) имеют явные преимущества перед традиционными решениями (плиты с воздушной прослойкой и плиты, в которых имелись пустоты правильной геометрической формы).
Выводы
Проведенное исследование подтверждает перспективность применения модифицированных цементно-песчаных матриц (ЦПМ) с ауксетической структурой для разработки усовершенствованных защитных систем. Полученные результаты создают основу не только для оптимизации существующих конструкций, но и для проектирования новых, более надежных решений, способных эффективно противостоять динамическим нагрузкам на СС.
Важным этапом работы стало построение регрессионной модели, устанавливающей количественную зависимость между напряжениями в плите покрытия СС и ключевыми факторами (X1 X2, X3). Проведенный анализ показал, что оптимальное сочетание геометрических параметров конструкции — увеличение толщины стенок до 8,6 мм при шестикратном масштабировании ячеек — обеспечивает минимальный уровень динамических нагрузок. Экспериментально подтверждено, что данная конфигурация позволяет снизить напряжения до 2,25 МПа, что свидетельствует о высокой эффективности предложенного решения для защиты сооружений от динамических воздействий и подтверждает корректность выбранных параметров модификации.
1. Stolyarski T., Nakasone Y., Yoshimoto S. Engieneering Analysis with ANSYS Software. 2nd ed. Oxford: Elsevier, 2018. 526 p.
2. Schwerdtfeger J., Heinl P., Singer R. F. , KörnerAuxetic C. Auxetic cellular structures through selective electron beam melting // Phys Status Solidi B. 2010. Vol. 247. I. 2. Pp. 269–272. DOI: https://doi.org/10.1002/pssb.200945513 EDN: https://elibrary.ru/OFDUMP
3. Ren X. et al. Auxetic metamaterials and structures: A review / X. Ren, R. Das, P. Tran, T.D. Ngo, Y.M. Xie // Smart Materials and Structures. 2018. Vol. 27. No 2. Article number 023001. DOI: https://doi.org/10.1088/1361-665X/aaa61c
4. Bell J., Zhang Y.X., Soe K., Hermes P. High Velocity Impact Behaviour of Hybrid-Fiber Engineered Cementitious Composite Panels // Advanced Materials Research. 2012. Vol. 450–451. Pp.563–567. DOI: https://doi.org/10.4028/www.scientific.net/AMR.450-451.563
5. Kelkar P. U. et al. Cellular auxetic structures for mechanical metamaterials: A review / P.U. Kelkar, H.S. Kim, K.-H. Cho, J.Y. Kwak, C.-Y. Kang, H.-C. Song // Sensors. 2020. Vo.l 20. Article number 3132. DOI: https://doi.org/10.3390/s20113132 EDN: https://elibrary.ru/ACDQBP
6. Chen D., Zheng X. Multi-material additive manufacturing of metamaterials with giant, tailorable negative Poisson’s ratios // Scientific Reports. 2018. Vol. 8. Article number 9139. DOI: https://doi.org/10.1038/s41598-018-26980-7 EDN: https://elibrary.ru/JUSAXH
7. Chen W.F. Plasticity in Reinforced Concrete. McGraw-Hill : J. Ross Publishing, 2007.
8. Albertini F. et al. Computational investigation of the effective mechanical behavior for 3D pre-buckled auxetic lattices / F. Albertini, J. Dirrenberger, A. Molotnikov, C. Sollogoub // Journal of Applied Mechanics. 2019. Vol 86. no 11. Article number 111003. DOI: https://doi.org/10.1115/1.4044542 EDN: https://elibrary.ru/XLHPXG
9. Zhao X. Dynamic crushing of double-arrowed auxetic structure under impact loading / X. Zhao, Q. Gao, L. Wang, Q. Yu, Z.D. Ma // Materials & Design. 2018. Vol. 160. Pp. 527–537. DOI: https://doi.org/10.1016/j.matdes.2018.09.041



















