г. Санкт-Петербург и Ленинградская область, Россия
г. Санкт-Петербург и Ленинградская область, Россия
студент
-, г. Санкт-Петербург и Ленинградская область, Россия
УДК 69.059.22 Повреждения
ГРНТИ 67.01 Общие вопросы строительства
ББК 308 Монтаж, эксплуатация, ремонт машин и промышленного оборудования
Целью данной статья является развитие теоретических основ оценки несущей способности конструкций с использованием вибрационного метода, установление точного значения положения нейтральной линии в процессе эксплуатации железобетонных конструкций. В ходе исследования применялись методы математического моделирования, основанного на известных теоретических выражениях, и сравнение полученных результатов с экспериментальными данными. В работе рассматривались конструкции с разным уровнем несущей способности, а именно балка без дефектов, балка с небольшими трещинами и балка с магистральной трещиной. Полученные экспериментальные значения остаточной высоты сечения бетона и высоты сжатой зоны достаточно точно совпадают с данными математического моделирования для этих характеристик. Полученные результаты позволят приблизиться к решению задачи теоретического обоснования вибрационного метода обследования железобетонной конструкции, усовершенствования методов его проведения и повышения точности получаемых результатов.
несущая способность, вибрационный метод, железобетонные конструкции, дефекты
Широкое применение железобетонных конструкций (ЖБК) в качестве несущего остова зданий началось примерно с 60-х годов прошлого века и насчитывает более 70 лет. За столь длительный период эксплуатации в конструкциях появились дефекты различного типа. В настоящее время, одним из актуальных вопросов является вопрос оценки их технического состояния в соответствии с ГОСТ 31937-2024. Использование современных приборов неразрушающих методов контроля позволяет определять лишь физико-механические характеристики ЖБК, и потом с помощью расчётных формул оценивать их несущую способность. Одним из способов оценивания несущей способности конструкций, без применения расчётных методов, является вибрационный метод [1–3].
Для теоретического обоснования вибрационного метода неразрушающего контроля железобетонных конструкций [1, 4], путем измерения частот колебаний и геометрических параметров конструкции необходимо точно понимать в какой степени в работе данной ЖБК задействованы ее элементы. Какая доля нагрузки приходится на бетон, а какая на арматуру?
Ключевым параметром для определения этих соотношений является положение нейтральной линии сечения, или высота сжатой зоны бетона x [3,5]. Расчеты этого параметра, согласно нормативной документации, позволяют рассчитать значение нейтральной линии для состояния близкого к разрушению конструкции, что не приемлемо для целей диагностики.
Согласно СП 63.13330.2018 пространственная жесткость железобетонной балки определяется по формуле:
|
|
(1) |
где
| $$ k_b=\frac{0,15}{\phi_I\cdot(0,3+\delta_e)} $$ |
где ϕl — коэффициент, учитывающий влияние длительности действия нагрузки;
Запишем уравнение жесткости сечения железобетонной балки относительно уровня нейтрального слоя, так как поворот сечения осуществляется именно относительно этой линии.
| $$I(x)=\frac{b}{3}\cdot x^3+[(h_0-\delta)-x]^3,$$ |
(2) |
| $$ I_s(x)=I_{sc}+I_s+A'_{sx}-a'2+A_sh_0-x^2, $$ |
(3) |
где x — высота сжатой зоны;
δ — глубина трещины;
Значения
Подставив выражения (2), (3) в исходное выражение (1) получаем формулу для оценки жесткости железобетонной балки в зависимости от положения нейтрального слоя или высоты сжатой зоны бетона:
|
$$D=k_bE_b\frac{b}{3} \cdot (x^3+[(h_0-\delta)-x]^3+k_sE_s(A'_s(x-a')^2+A_s(h_0-x)^2),$$ |
(4) |
Для удобства записи введем коэффициенты
|
|
(5) |
|
|
(6) |
|
$$a_3=\frac{k_bE_bb(h_0-\delta)^3}{3}+k_sE_s(A'_sa'^2+A_sh^2_0).$$ |
(7) |
Конечное уравнение запишем в виде:
|
|
(8) |
Для примера возьмём железобетонную балку 1ПБ-10-1П, характеристики которой представлены в Таблице 1. Схема загружения и сечение балки представлено на Рис. 1 и 2 соответственно.
Таблица 1
Оценка эффективности компонентов добавки
|
Марка |
Размеры, мм |
Масса, кг |
Es, МПа |
Eb, МПа |
|||||||||
|
L |
L0 |
b |
b' |
h |
h0 |
a |
a' |
d |
δ |
||||
|
1ПБ-10-1П |
1030 |
930 |
120 |
80 |
65 |
53 |
12 |
18 |
4 |
Var(0…h0) |
20 |
3х |
2х |

Рис. 1. Расчетная схема балки 1 ПБ-10-1П
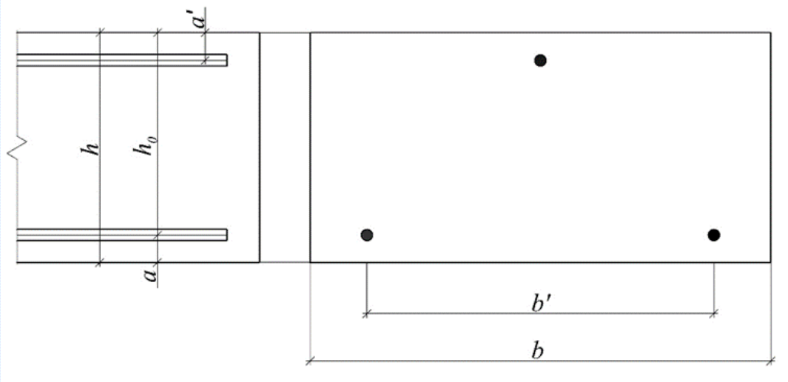
Рис. 2. Сечение балки 1 ПБ-10-1П
Применим уравнение (8) к исходной балке и определим те состояния, в которых жесткость достигает своих минимальных/максимальных значений и не может выходить за отведенные границы.
Уравнение (8) является квадратным, график которого представляет собой параболу, ветви которой направлены вверх, а вершина имеет координаты (m, n), где
| $$m=-\frac{-a_2}{2 \cdot a_1},$$ |
(9) |
|
$$n=-\frac{a_2^2-4 \cdot a_1 \cdot a_3}{4 \cdot a_1},$$ |
(10) |
Необходимо найти экстремумы функции D(x,
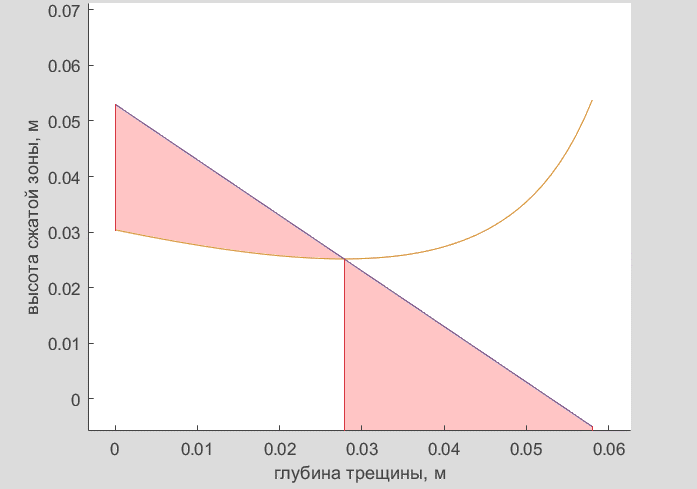
Рис 3. Область допустимых значений высоты сжатой зоны бетона
Назовем трещины, глубина которых попадает в 1 и 2 области трещинами первого и второго типа соответственно, и исследуем распределение напряжений в сечении и высоту сжатой зоны бетона. Для этого смоделируем в программном комплексе «ELCUT» данные случаи (Рис. 4–6), рассматривая железобетонную балку как упруго-деформируемую систему.
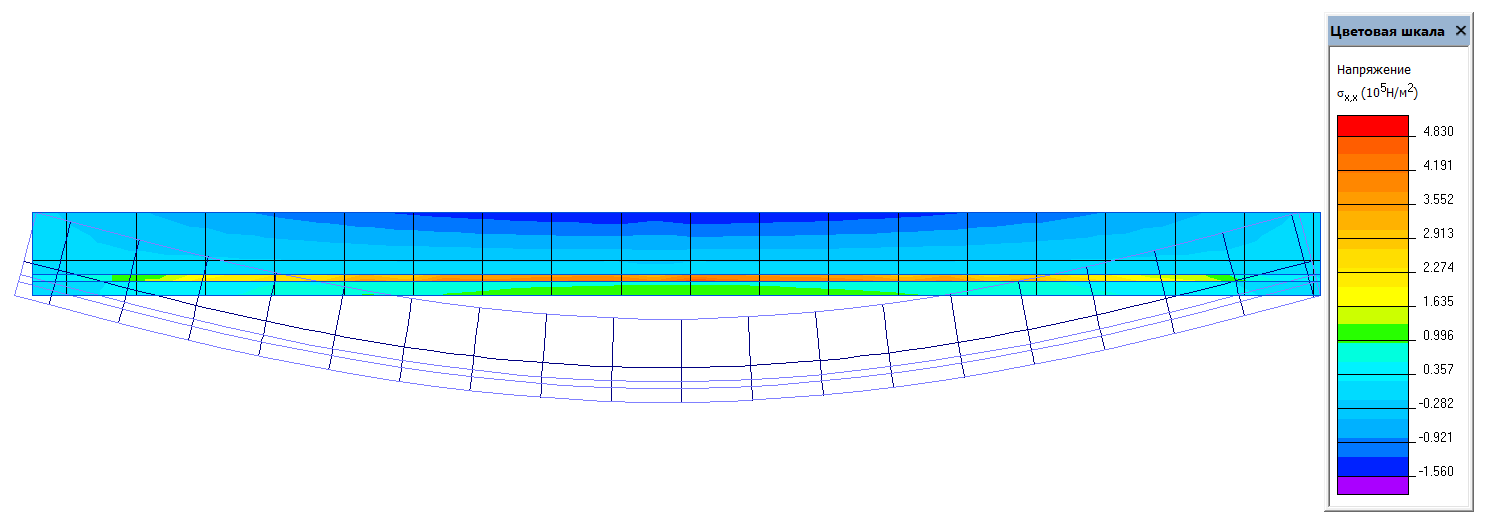
Рис. 4. Модель балки без трещин
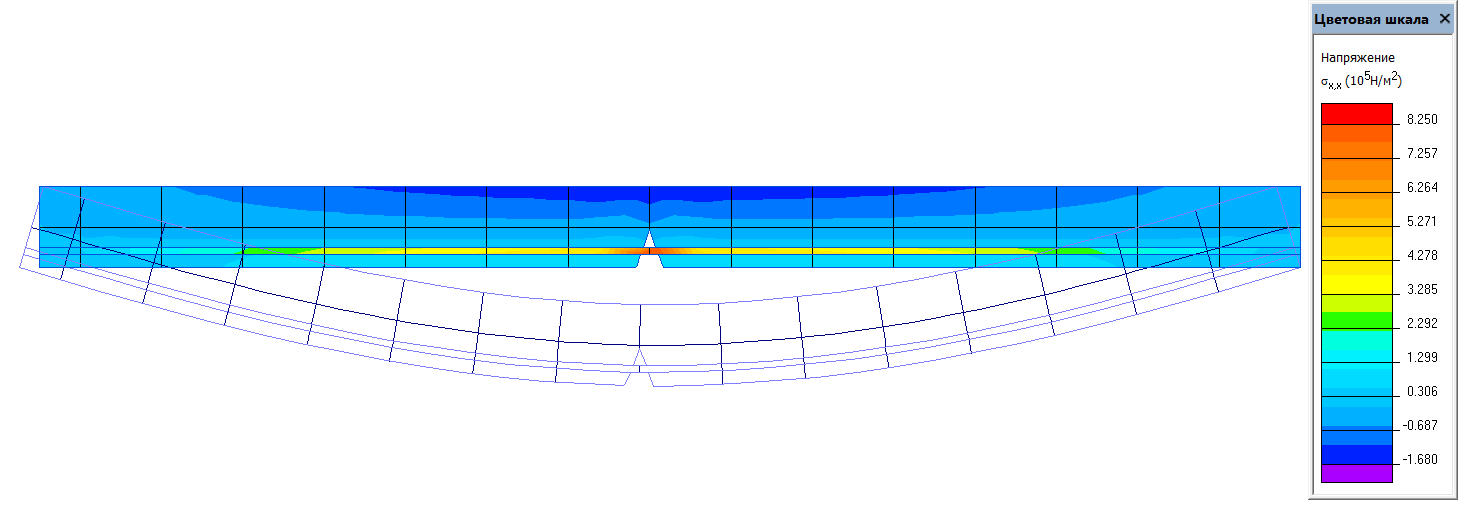
Рис. 5. Модель балки с трещиной первого типа
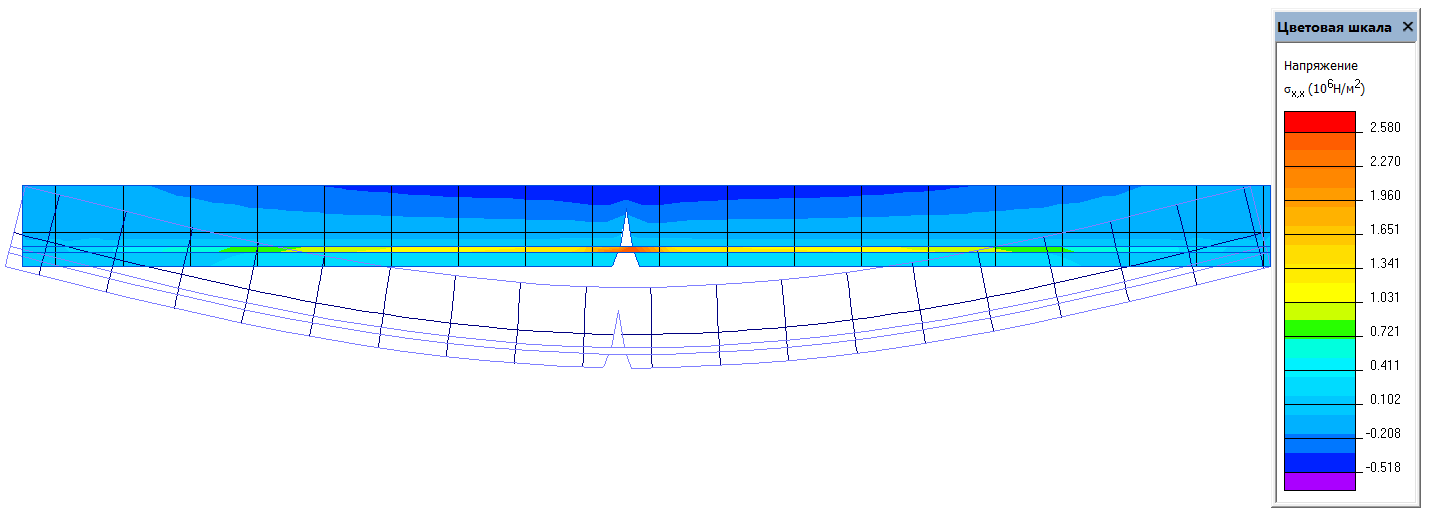
Рис. 6. Модель балки с трещиной второго типа
Полученные результаты представлены в Табл. 2.
Таблица 2
Результаты исследования
|
Тип трещины |
Результаты моделирования |
Результаты теоретического расчета |
|||
|
Глубина |
Остаточная высота |
Высота сжатой |
Максимальное значени |
Минимальное значение |
|
|
Без трещины |
- |
60,00 |
29,65 |
53,00 |
30,00 |
|
Первый тип |
23,00 |
37,00 |
27,33 |
35,00 |
27,00 |
|
Второй тип |
43,00 |
17,00 |
15,31 |
17,00 |
0,00 |
Вывод: таким образом, с использованием математических зависимостей, были определены границы нахождения фактического значения высоты сжатой зоны бетона x, которые подтверждаются моделированием с использованием метода конечных элементов.
Полученные результаты позволят приблизиться к решению задачи теоретического обоснования вибрационного метода обследования железобетонной конструкции, усовершенствования методов его проведения и повышения точности получаемых результатов.
1. Исхаков Ш.Ш., Ковалев Ф.Е., Мохнаткин А.П., Старчуков Д.С. Становление и развитие вибрационных систем мониторинга технического состояния несущих элементов стартовых сооружений. 2015. 110 с.
2. Исхаков Ш. Ш., Ковалёв Ф. Е., Зарин С. В. Об эффективности метода вибрационной диагностики элементов строительной части стартовых сооружений // Известия тульского государственного университета. Технические науки. 2018. Вып. 10. С. 431–441. EDN: https://elibrary.ru/YRBIPR
3. Исхаков Ш. Ш., Ковалёв Ф. Е., Зарин С. В. Учет трещинообразований бетона в вибрационной диагностике пролетных железобетонных конструкций // Труды Военнокосмической академии имени А. Ф. Можайского. Вып. 2018. Вып. 663. С. 99–104.
4. Исхаков Ш. Ш., Ковалев Ф.Е., Косенков Р.Э., Мохнаткин А.П. Проблемы оценивания надежности и безопасности эксплуатируемых сооружений наземной космической инфраструктуры и идентификации их технических состояний // Известия ПГУПС. 2016. Т. 13, вып. 4(49). С. 592–599. EDN: https://elibrary.ru/YFUDFR
5. Ковалев Ф.Е., Мохнаткин А.П. Методика оценивания допредельных и предельных состояний пролетных железобетонных конструкций стартовых сооружений по параметру высоты сжатой зоны бетона. // Труды Военно-космической академии имени А.Ф.Можайского. 2022. № 681. 170-175 с. EDN: https://elibrary.ru/BXPNZC



















